Go to the Prior Tip
Goal Seek Method for Fast IRR Solutions
Go to the Next Tip
The Perfect Bet by Adam Kucharski
Return to MaxValue Home Page
High-payoff lottery tickets fun examples of people winning extreme wealth. Wikipedia (checked Jan 2020) listed 47 PowerBall, Mega Millions, or The Big Game jackpots where the award cash value was over $300 million (among 17 tickets). The HGTV channel has a “My Lottery Dream Home” series, where the show‘s host helps winners buy fabulous new homes with part of their big winnings.
Big These payout amounts are off the utility charts for 99.999% of the world‘s population. As such, big payout lotteries provide examples of where the exponential utility function (EUF) may not apply.
Several years ago, I had a discussion with a colleague, Tim Nieman, who owns a nice boat. Let’s presume that, if Tim gains enormous wealth, he will buy much, much bigger boat: a yacht!
Fun facts about the (deceased) Microsoft co-founder Paul Allen’s super yacht. A billion doesn‘t go as far as you might think.
I proposed this question: What fraction (F) of your net worth (NW) would you be willing to bet on this 50:50 gamble?
Win: Gain $100 million
Lose: Lose F x NW.
Assuming an EUF shape, these lottery parameters (F and NW), and Tim’s answer, we can easily solve for r using Microsoft® Excel®’s Goal Seek tool.
Tim’s answer was “1/7” of his NW. We set up Excel to find r that makes CE = $0, and we find that Tim’s answer imputes an r = .206 x NW.
I presented a similar question to another friend, wealthy by most standards. “How much, as a fraction of your net worth, would you willing to risk on a 50:50 gamble with a $1 billion win payoff. He responded:
When the win value is much greater than r, then U(win value) ≈ r. Then, we can solve for r given NW and F. The formula works out to:
r = F x NW / Ln(2) = 1.443 x F x NW
So, his r appears to be about 1.443 x (1/20) x NW = .072 NW ≅ (1/14) x NW.
I set out to explore this investment situation with a very high potential outcome. In the first version of this Tip, I generated many random combinations and used Matlab‘s contour function for the chart.
I was unhappy with the chart quality. This time, at steps at different r/NW ratios, I swept:
Payoff Multiple of Net Worth for specific Bet Fractions of Net Worth; and
Bet Fractions of Net Worth for specific Payff Multiples of Net Worth.
Here are several observations:
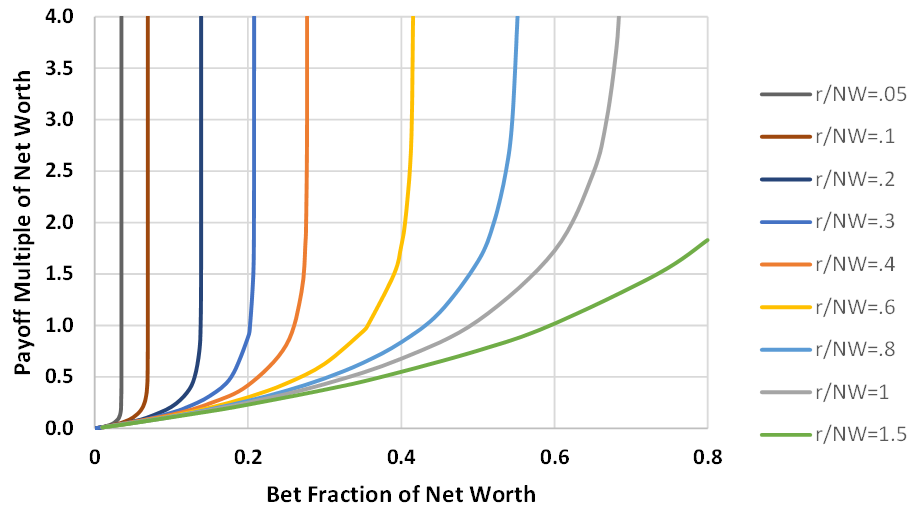
This next figure is the same as above, zoomed-in to the lower-left portion. This is the region of interest for most people. A typical order-of-magnitude r / NW is about 0.2. That is, r is about 1/5 of NW.
Contour chart of r’s expessed as r / NW. This assumes a 50:50 gamble. The Payout Multiple of Bet Amount, y-axis, is the multiple of the bet amount that is the win amount. The Bet Fraction is the fraction of NW the person is willing to risk. The contour values are selected r / NW.
I’ve worked with the EUF for years. Still, I was a surprised at how quickly the r / NW contours turn vertical with even modest Payoff Multiples. The perceived value—utility—diminishes quickly as the payoff approaches r. A plausible situation would be be an investor with an r of 0.2NW. A payoff of just 0.45NW would be at 90% of her maximum utility. A payoff of just 0.60NW would realize 95% of her maximum utility. This isn’t of too much concern in normal investment decisions, because few projects would have success values greater than r. So, except in extreme situations, the EUF works well.
When I was young, one of my favorite TV shows was The Millionaire. Each episode was about how an ordinary person’s life changed after receiving an unexpected $1 million, tax-free. It was fun to imagine how it would feel to be “the next millionaire.” Mom said that few people would ever be able to consume a million dollars by spending on themselves. She may have been right. $1 million then is about $9 million in 2020 dollars (based upon U.S. Consumer Price Index).
With excess wealth, I think most people would shift their thoughts from self-indulgence toward altruism. Imagine how much good you could do by giving large amounts to your charities, community, nation, or the world.
Would you risk your entire NW for a chance to save, say, 100 lives? Would you risk your life? Risk both? I would, though this isn’t for everyone. Suppose you have a Chernobyl or Fukushima to clean up, and the cleaners face certain death from radiation. If you’re willing to pay, say, $5 million to my designated causes, then I’ll step up to be one of your cleanup crew.
Perhaps the EUF still applies. For self-serving, financial decisions, r is typically on the order of NW /5. But, for an ethical risk policy involving human lives, perhaps r should instead be on the order of someone’s life value.
Wikipedia‘s Trolley Problem article discusses ethics in a life-risking decision dilemma.
If you are interested in determining your r for risky economic decisions, I suggest that you check out the online Utility Elicitation Program app. UEP is available (free, except to my competitors) at https://www.maxvalue.com/online.htm
—John Schuyler, Dec 2017 revised Feb 2020 deleting the table and replacing the chart.
© 2017-2020 John R. Schuyler. Permission to copy with reproduction of this notice.