Utility Function for Risk Policy

Utility Function

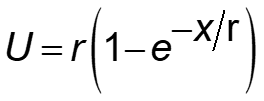
Risk policy provides a way to make logical, consistent trade-offs between risk and value.

Daniel Bernoulli established a mathematical foundation for utility functions in 1738. "Utility" is a term economists and psychologists use to describe value. A utility function, or curve, translates an objective measure, say $ or NPV $, into how the person feels about that quantity.

Bernoulli surveyed people and found that, unsurprisingly, they are risk-averse. He posited that one's risk tolerance is approximately proportional to wealth. No surprise: wealthy people are more able to tolerate more risk.

While there are competing formulas for utility functions, the "exponential utility function" (EUF) is the most practical. It is named for the exponential term in the formula. EUF is the easiest and most consistent expression of risk attitude and, hence, risk policy.

I recommend this equation form:

where:

U =	utility value in risk-neutral dollars (RN$) (in the U.S. and other countries using the $ symbol)
x =	objective outcome value, usually NPV $
r =	risk tolerance coefficient, typically on the order of 1/5 of the decision maker’s or organization’s net worth

There are at least two other EUFs that are equivalent but have less meaningful units.

An aside: The EUF equation, above, is similar to the exponential equation for present value discounting that appears in many textbooks..

Here is an EUF scaled for r = $5,000:

    Exponential Utility Function. This concave function represents a complete risk policy if the
    outcomes are objectively valued in NPV or NPV-equivalents. The 45° line is for reference
    and is the utility function for a risk-neutral person. The red arrows show determining
    the utility of $4,000 NPV. The Excel equation is =5000*(1-EXP(-4000/5000)), which returns RN$2,753.

An aside: There are other possible utility functions. Mathematicians can be very creative and elaborate. Reseachers have elicited utility preferences with a step-sequence of lotteries or by looking at historical decisions. Most produce abysmal curves—not very workable, in my opinion.

Only an EUF has:

The same buy and sell values. The asset or project value doesn't suddenly change when you make a deal.
The risk-attitude-adjusted value is the certain equivalent (CE, described in the next section). This EUF has the delta property:
Adding $x to all the outcomes increases the CE by $x. Similarly, subtracting $x from all the outcomes reduces the CE by $x.

Though not unique to EUF, it is convenient that a positive outcome has positive utility, and a negative outcome has a negative utility.

r is just a scaling factor that determines the curvature of the utility function. On average, people with 10 times as much wealth have r 's 10 times as high. Conceptually, Warren Buffet and I have the same utility curve shape. Mr. Buffet's utility function just has much larger numbers on his x- and y-axis scales.

The EUF has utility units in "risk-neutral dollars" (RN$). Here are examples relating utility units to dollars:

For small values, numerically, U(x) = x, though in different units.
RN$100k feels 100k times better than $1.
RN$100k feels as good as -RN$100k feels bad:
A decision maker with this r would be indifferent about a coin toss with outcomes RN$100k and -RN$100k.
The $RN units are more-pleasing. For outcomes small compared to r, the utility value U(x) (though $RN units) is about the same as $x. The utility value diminishes for large gains (law of diminishing marginal utility) and magnifies for large losses.

Expected value utility is the probability-weighted utility outcome. I conform to common practice and call this expected utility with the abbreviation EU.

The expected utility decision rule is: Choose the alternative with the highest r.

Though this is sufficient for decision making, I recommend one more step: Convert rs to certain equivalents (CEs). The CE is the cash-in-hand value of a risk.

Flow diagram of evaluating a risk's EU and CE.

The Analysis Process with Utility.

Here are the steps:

Calculate the NPVs for possibles outcomes.
Calculate EMVs for each alternative for comparison.
Convert NPVs to utility units using the decision maker's utility function.
For each alternative, calculate EU.
Convert EUs to CEs (using the formula below).
Choose the alternative with the highest CE.

The inverse equation, translating EU into CE is:

The meaning of CE:

If an alternative has no uncertainty, then its CE is the NPV.
The CE of a risky project or asset is the most you would be willing to pay to acquire it.
Or, if you already own the project or asset, CE is the smallest amount for which you would be willing to sell it.

The EUF has constant risk aversion and features:

The CE is the same, whether buying or selling the risky asset. The asset’s value doesn’t suddenly change as soon as you close a transaction.
Adding $x to all the outcomes increases the CE by $x. Similarly, subtracting $x from all the outcomes decreases the CE by $x. This is the delta property that is unique to EUF. Of course, the EMV decision policy also has this property with the special EUF as a 45° line.

Determining r is typically through “lottery” experiments. The link takes you to one example.

Utility Elicitation Program is a free (for most users) automated tool to help you self-assess r's through several lottery types. Access UEP at http://www.maxvalue.com/online.htm.